Aprenda estimativas com o game 'Ice Ice Maybe'
Faixa etária: 9 a 14 anos
CONHECIMENTOS MATEMÁTICOS ABORDADOS
- Fazer estimativas com operações de adição, subtração, multiplicação e divisão;
- Fazer estimativas com porcentagens;
- Fazer estimativas com frações.
BNCC
OBJETOS DE CONHECIMENTO | HABILIDADES |
Problemas: adição e subtração de números naturais e números racionais cuja representação decimal é finita | (EF05MA07) Resolver e elaborar problemas de adição e subtração com números naturais e com números racionais, cuja representação decimal seja finita, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos. |
Problemas: multiplicação e divisão de números racionais cuja representação decimal é finita por números naturais | (EF05MA08) Resolver e elaborar problemas de multiplicação e divisão com números naturais e com números racionais cuja representação decimal é finita (com multiplicador natural e divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos. |
Frações: significados (parte/todo, quociente), equivalência, comparação, adição e subtração; cálculo da fração de um número natural; adição e subtração de frações | (EF06MA07) Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes. (EF06MA08) Reconhecer que os números racionais positivos podem ser expressos nas formas fracionária e decimal, estabelecer relações entre essas representações, passando de uma representação para outra, e relacioná-los a pontos na reta numérica. (EF06MA09) Resolver e elaborar problemas que envolvam o cálculo da fração de uma quantidade e cujo resultado seja um número natural, com e sem uso de calculadora. (EF06MA10) Resolver e elaborar problemas que envolvam adição ou subtração com números racionais positivos na representação fracionária. |
Cálculo de porcentagens e de acréscimos e decréscimos simples | (EF07MA02) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros. |
COMO JOGAR
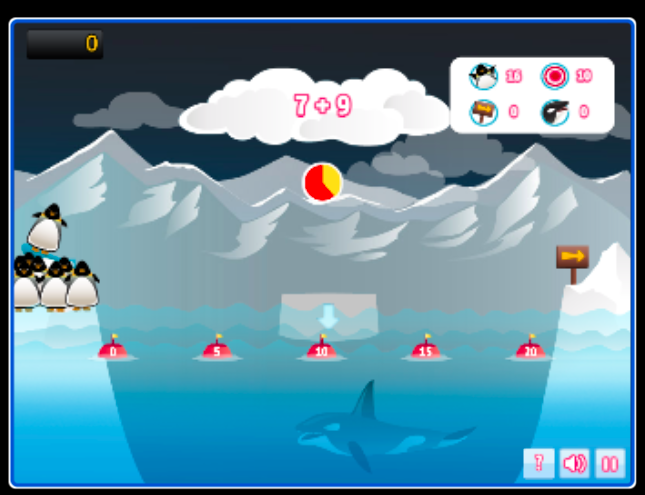
Use suas habilidades de estimativa e aproximação para posicionar o iceberg corretamente e ajudar os pinguins a atravessar o mar congelante!
Neste jogo, os pinguins irão viajar pelo perigoso Oceano Estim — um vasto mar gelado patrulhado por baleias orcas sempre famintas. Posicione corretamente os icebergs e ajude os pinguins a pular com segurança de uma margem para outra. Ajude quatro bandos de pinguins a chegar à Ilha do Verão.
Os pinguins começam na margem esquerda, onde ergueram uma catapulta para impulsioná-los até a margem oposta. No entanto, a catapulta não é poderosa o suficiente para arremessá-los para o outro lado do canal. Portanto, eles precisarão que você posicione estrategicamente o iceberg no mar para que o bando consiga chegar com segurança à outra geleira.
As questões matemáticas aparecem na parte superior da tela, junto com um cronômetro. Usando suas habilidades de estimativa e aproximação, mova o mouse para a esquerda e para a direita para movimentar o iceberg e clique no local que desejar posicioná-lo. Responda corretamente a pergunta que aparece na nuvem e descubra onde o iceberg deve ser posicionado!
- Se o seu iceberg estiver posicionado próximo o suficiente da resposta correta, o pinguim salta com segurança.
- Caso contrário, o pinguim cai nas águas infestadas de baleias e se perde!
Se o tempo acabar antes de você posicionar o iceberg, a catapulta arremessa automaticamente o pinguim e ele cai na água no ponto correspondente à resposta correta.
Você só pode colocar um iceberg de cada vez (a cor do cursor indica se você pode colocar um iceberg ou não).
Cada bando começa a jornada com 16 pinguins. Tome cuidado, pois à medida que você passa de fase, os seus erros também serão levados para o próximo nível e por isso será mais difícil atingir a meta. Preste bastante atenção, pois ao longo da viagem você pode encontrar ovos que aumentam o número de pinguins no bando!
PONTUAÇÃO
Existem 4 caminhos neste jogo. Conclua cada caminho para alcançar pontuação desejada e ganhar uma medalha de Bronze, Prata ou Ouro.
- Caminho 1: Estimativa com adição e subtração >> Conclua o caminho dos Pinguins-Imperadores >>> 24 000 (B), 60 000 (P), 120 000 (O)
- Caminho 2: Estimativa com multiplicação e divisão >> Conclua o caminho dos Pinguins-de-Adélia >>> 24 000 (B), 60 000 (P), 120 000 (O)
- Caminho 3: Estimativa com porcentagem >> Conclua o caminho dos Pinguins-Macaroni >>> 24 000 (B), 60 000 (P), 120 000 (O)
- Caminho 4: Estimativa com frações >> Conclua o caminho dos Pinguins Azuis >>> 24 000 (B), 60 000 (P), 120 000 (O)
Cálculo da pontuação
- A pontuação geral é a soma das pontuações mais altas alcançadas em cada nível.
- Seu melhor desempenho em cada nível é registrado.
- Observe que à medida que seu multiplicador aumenta, o cronômetro diminui — ou seja, vai ficando mais difícil se manter na zona de pontuação alta!
- E atenção: o cronômetro zera se você perder um pinguim!
ESTRATÉGIAS MATEMÁTICAS
Adição e Subtração
- Arredonde números múltiplos de 10: ao lidar com números inteiros, você pode descobrir que arredondar os números para um múltiplo de 10 é uma maneira útil de se estimar o resultado.
- Muitas vezes é mais fácil adicionar do que subtrair: ao lidar com a subtração, geralmente é mais fácil adicionar do que subtrair. Por exemplo, o resultado de 121 − 78 pode ser estimado por 120 − 80. Começando com 80, você pode adicionar mais 40 para chegar em 120. Portanto, uma boa estimativa é 40.
- Arredonde números grandes para múltiplos de 100: ao lidar com números grandes que incluem decimais, você geralmente pode fazer uma estimativa rápida arredondando para a centena mais próxima. Por exemplo, 128,4 + 187,3 pode ser rapidamente estimado em 300.
Multiplicação e Divisão
- Tabuada para auxiliar na divisão: você pode usar seu conhecimento de tabuadas para ajudar com questões de divisão. Por exemplo, 35,4 ÷ 6 pode ser estimado sabendo que 6 × 6 dá 36.
- Utilize fatos da divisão: ao estimar divisões mais difíceis, você pode tentar usar alguns atalhos. Por exemplo, ao estimar o resultado da divisão 132,5 ÷ 6,23, você pode primeiro calcular 12 ÷ 6 que resulta em 2, mas a estimativa é dez vezes maior, pois 132,5 está relativamente próximo de 120. Então uma boa estimativa é 20.
Frações
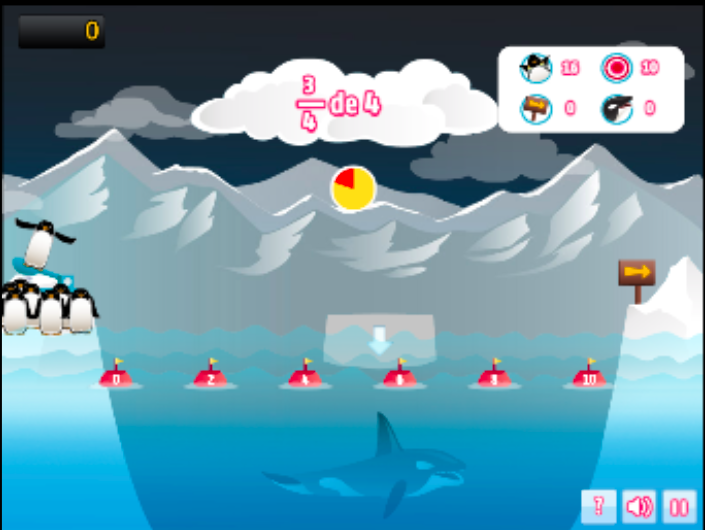
- Compare a fração com a metade: ao estimar uma fração de um valor, muitas vezes você pode comparar a fração à metade. Por exemplo, ⅓ de 41,4 será menos da metade de 40. Portanto, coloque o iceberg logo abaixo de 20.
- Frações próximas de 1: se a fração for próxima de 1, por exemplo, 9⁄10 de 43, então a resposta será um pouco abaixo de 43 — neste caso, uma estimativa em torno de 40 seria boa.
Porcentagens
- Divida por 10 para obter 10%: para calcular 10% de um valor, divida-o por 10. Por exemplo, para calcular 10% de 450, divida 450 por 10 e obtenha 45.
- Use 10% para calcular outras porcentagens: calcular 10% do valor pode ajudar ao tentar calcular outras porcentagens. Por exemplo, para estimar 28,1% de 502, primeiro calcule 10% de 500, que é 50. Como 28,1% é quase 30%, aproxime 28,1% por 30% . Para determinar 30% de 500, calcule 50 × 3 = 150. Portanto, 150 será uma boa aproximação para 28,1% de 502.
OUTRAS ESTRATÉGIAS
- Não perca tempo (e pontos!) buscando as respostas exatas: Embora as adições e subtrações possam ser simples, é quase certo que você não terá tempo para calculá-las com exatidão! Experimente arredondar os números da pergunta para um algarismo significativo. Fazer o cálculo com os valores arredondados será muito mais rápido e fácil e lhe dará uma ideia de onde está a resposta exata. Por exemplo, se a pergunta for 6,1 × 4,2, pense em 6 × 4. Isso indica que a resposta exata será próxima de 24.
- Em seguida, pense se a resposta será maior ou menor que o número que você obteve: Por exemplo, está claro que 6,1 × 4,2 será um pouco maior que 6 × 4 e que 5,8 × 3,9 será um pouco menor que 6 × 4. Você deve levar isso em consideração ao posicionar o iceberg.
- Se você estiver calculando porcentagens ou frações de números, tente visualizar a posição do número que você precisa em uma reta numérica. Por exemplo, se a questão for ⅓ de 74,4 imagine onde 74,4 está na reta numérica e pense sobre onde está ⅓ do caminho para esse número.
