Estimation using 'Ice Ice Maybe'
CURRICULUM AREAS COVERED
Ages 9-14
- Estimate with addition, subtraction, multiplication and division
- Estimate a percentage of a number
- Estimate a fraction of a number
HOW TO PLAY
Use your estimation and approximation skills to correctly position iceberg which helps penguins cross the icy sea.
In this game, the penguins' vacation migration sees them journey across the perilous Estim Ocean, a vast icy sea patrolled by ever-hungry killer whales. Correctly position floating icebergs and bounce the penguins safely from glacier to glacier. Help four waddles of penguins reach the holiday paradise of Summer Isle.
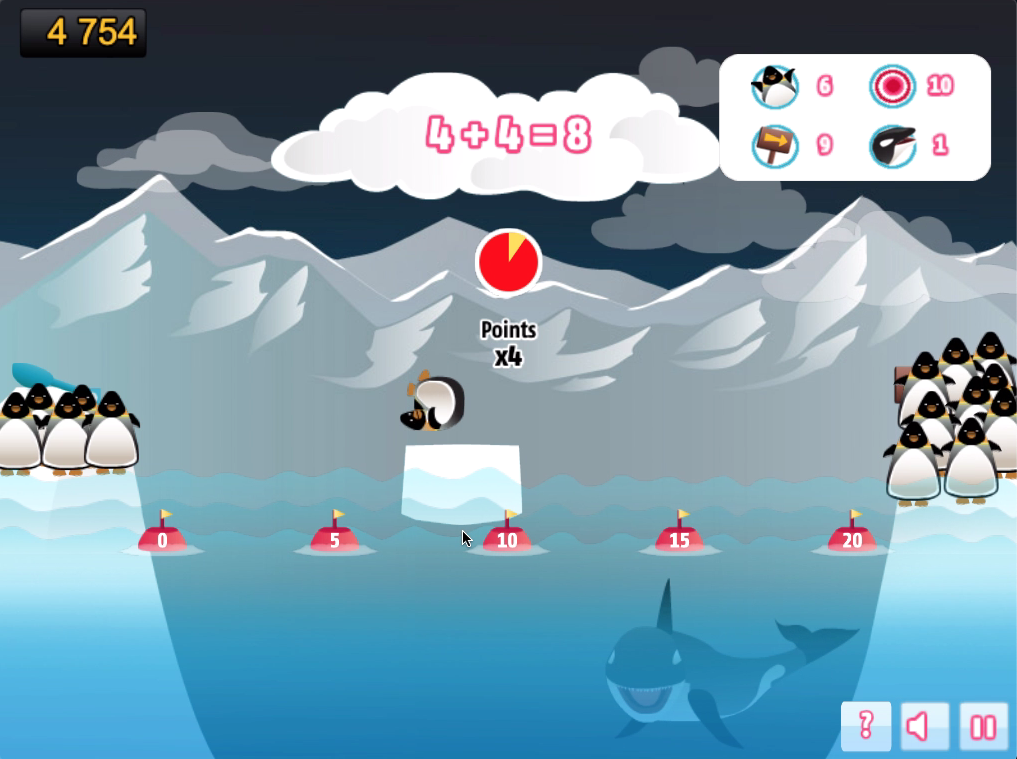
The penguins start on the left bank, where they've erected a pengopult. Unfortunately, it's not powerful enough to fling the penguins all the way to the safety of the opposite bank. So they will need to bounce off an iceberg in the sea to successfully get across.
Mathematical questions appear at the top of the screen, along with a clock. Using estimation and approximation skills, move your mouse left and right to move the iceberg along and click on the position to place the iceberg. The appropriate positioning is based on the question.
- if your iceberg is positioned close enough to the correct answer, the penguin bounces to safety;
- if not, the penguin tumbles into the whale-infested waters and is lost.
If the clock runs out before you position an iceberg, the pengopult launches automatically, and the penguin splashes down at the point corresponding to the answers.
You can only place one iceberg at a time (the cursor colour indicates whether you can place an iceberg or not).
Each waddle starts its quest with 16 penguins. Take care as any losses carry over to the next level, making the target tougher to meet. Occasionally you may find eggs which swell the waddle's number.
SCORING INFORMATION
There are 4 paths in this game. Complete the relevant path and achieve the Target Score to earn a medal (Bronze, Silver, Gold).
- Path 1: Estimate with addition and subtraction >> Complete the Emperor Penguins path >>> 24,000 (B), 60,000 (S), 120,000 (G)
- Path 2: Estimate with multiplication and division >> Complete the Adelie Penguins path >>> 24,000 (B), 60,000 (S), 120,000 (G)
- Path 3: Estimate a percentage of a number >> Complete the Macaroni Penguins path >>> 24,000 (B), 60,000 (S), 120,000 (G)
- Path 4: Estimate a fraction of a number >> Complete the Fairy Penguins path >>> 24,000 (B), 60,000 (S), 120,000 (G)
Scoring calculation
Your overall score is the sum of the highest scores you achieved on each completed level. Your best performance at each level is recorded and retained.
Note that as your multiplier increases, the timer decreases too - see how long you can stay in the high-scoring zone! The timer resets to its max value if you lose a penguin.
MATHS STRATEGIES
Addition and Subtraction
- Round whole numbers to the nearest 10. When dealing with whole numbers you may find that rounding the numbers to the nearest 10 is a useful way to estimate the result.
- It is often easier to add instead of subtract. When dealing with subtraction it is often easier to add on rather than subtract. For example, 121 − 78 can be estimated as 120 − 80. Starting with 80 you can add on 40 more to make 120. So the estimate is 40.
- Round large numbers to the nearest 100. When dealing with large numbers that include decimals you can often make a quick estimate by rounding to the nearest hundred. For example, 128.4 + 187.3 can be quickly estimated to 300.
Multiplication and Division
- Times Tables to help with Division. You can use your knowledge of times tables to help with division questions. For example, 35.4 ÷ 6 can be estimated by knowing that 6 × 6 makes 36.
- Take short cuts. When estimating more difficult divisions you can try to use some short cuts. For example, take 132.5 ÷ 6.23. You can think of this as 12 ÷ 6 to make 2, but the estimate is actually ten times larger, giving an estimate of 20.
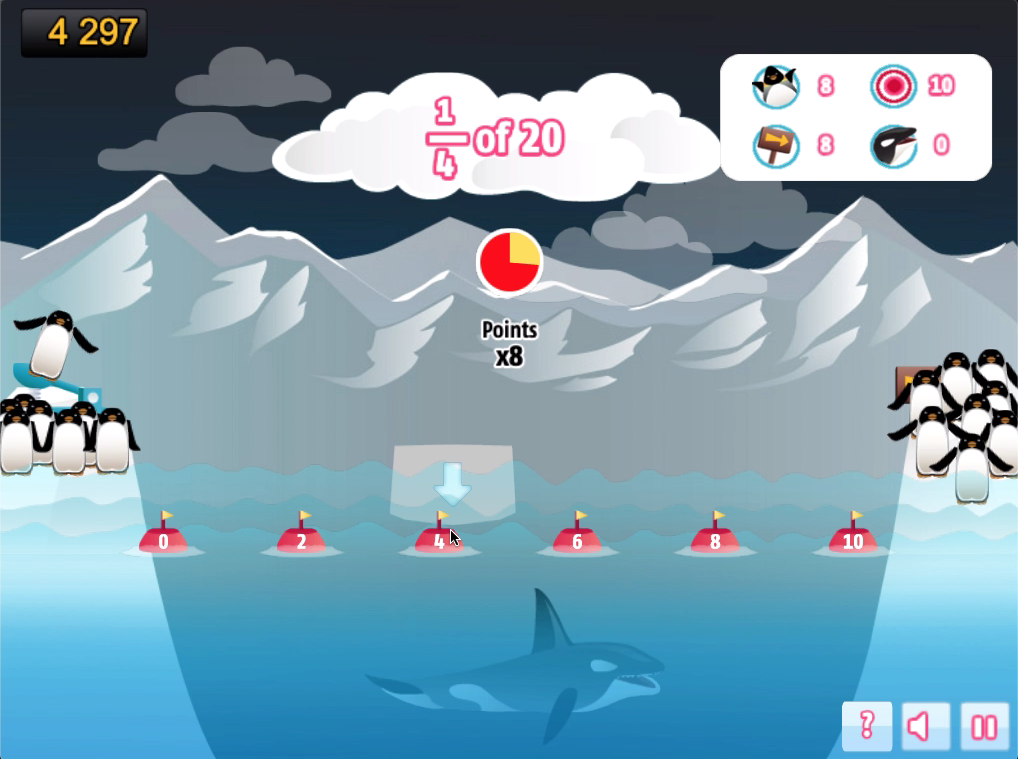
Fractions
- Compare the fraction to a half. When estimating a fraction of an amount, you can often compare the fraction to a half. For example, ⅓ of 41.4 will be less than half of 40. So place the iceberg just below 20.
- Fractions close to 1. If the fraction is close to 1, for example, ⁄ of 43, then the answer will be just below 43 – in this case, an estimate around 40 would be good.
Percentages
- Divide by 10 to get 10%. You can find 10% of an amount by dividing the amount by 10. For example, to find 10% of 450, divide 450 by 10 to get 45.
- Use 10% to find other percentages. Finding 10% first can really help when trying to find other percentages. For example, to find 28.1% of 502, first estimate 10% of 500, which is 50. Then, as 28.1% is nearly 30%, find 30% by working out 50 × 3. An estimate of 150 will be a close approximation.
OTHER BASIC STRATEGIES
- Don't waste time (and points!) working out the exact answers. Although the additions and subtractions may be simple, you almost certainly won't have time to calculate them exactly!
- Try rounding the numbers in the question to one significant figure. Doing the calculation with the rounded values will be a lot quicker and easier and it will give you some idea of where the "real" answer is. For example, if the question is 6.1 × 4.2, think about 6 × 4 instead. This tells you that that the "real" answer will be near to 24.
- Next, think about whether the answer will be bigger than or smaller than the number you got For example, it's clear that 6.1 × 4.2 will be a bit bigger than 6 × 4 and that 5.8 × 3.9 will be a bit smaller than 6 × 4. You should take this into account when you position the iceberg. What about 6.1 × 3.9
- If you are taking percentages or fractions of numbers then try to visualise how much of the number you need on a number line. For example, if the question is ⅓ of 74.4 imagine where 74.4 is on the number line and think about where ⅓ of the way to that number is.
